kekule-for-scales
tags :: R:music, R:information-architecture
-
Thoughts about using kekule structure to denote musical scale
-
There are also commonalities between degeneracy of benzene rings and the modes of limited transposition in symmetric scales
-
Scales can be represented using regular polygons
- Whole step denoted like double bonds
- Half-step like single bonds
-
This gives you a minimalist scale representation that consists of all relevant information
- number of notes (is it diatonic, pentatonic or octatonic?),
- position of whole and half steps (is it a specific mode with raised notes)
- Emphasizes on circular nature of notes
Why tho?
I’ve come to depend a substantial amount on taking notes. It has resulted in a general improvement in my ability to think and retrieve thoughts. However, it falls flat in one specific case - when I want to make a note of musical ideas. Making a note of musical ideas is incredibly important to me, not only for all the reasons note-taking that is good for in general, but also the relief that comes from being able to offload a tune or rhythm stuck in head head and freeing up cognitive abilities to do other things with my life.
With that in mind, I fleshed out a set of expectations from a musical note taking system:
- A frictionless method of recording and retrieving notes
- Flexible w.r.t medium, allowing me to use it with or without a computer
- (Optional) Offers opportunity to view musical ideas in different context when reviewing
- Makes communicating ideas relatively easy
- Allows room for improvisation when performing the idea without necessarily
Thus far, I’ve relied on two systems, both of which come with their own forces of friction:
-
Voice Memo App On My Phone - Transfering voice memos and organizing copious amounts of them is a huge challenge. I would love to be able to tag and file ideas under specific categories. Additionally, most voice memo apps make it difficult to access the file outside their interface in any way other than emailing it to me and then downloading the file. This is so many levels of bureaucracy.
-
I also own a Zoom H1 recorder, which interestingly cuts through a lot of these problems with a one-click record feature, combined with the ability to transfer files via USB. This solves a lot of problems that a voice memo app presents, but invariably ends up being useless simply because I don’t have my pocket recorder with me all the time.
-
I also use DAWs (Ableton Live in my case) to quickly prototype ideas that are more than a beat or a melodic phrase. I do this by saving a skeleton project with MIDI tracks capturing rudimentary information about rhythms, melodies or chords. While this lends very well in terms of retrieval and organization, it requires a ton of overhead work before I can put an idea down. Most DAWs also are a cesspool of distraction presenting in the form of access to your entire sample and software-synth collection waiting to be tinkered with - which can quickly turn a note-taking session into a 2 hour long arrangement-related goat farm. It also requires me to be around a computer, which is not always the case. I’m more likely to find a piece of paper and a pen.
-
While I finally recognize the value of sheet music, it continues to be too elaborate a system for me to learn from scratch at this point. Music written on western sheet music notation also have certain meta-notations that I have little interest in adopting: such as the trebble and bass-clefs, time and key signatures etc. Often my ideas are far from concrete to the point of having these properties be set in stone. Sheet music in this way is a bit rigid.
-
A relatively flexible alternative is the Real Book style lead sheet that has minimalist representations of harmonies and melodies, giving a lot of room to improvise. It also gives you the excellent opportunity to re-interpret your original idea in new ways when you get back to it.
Pitch Wheels
Ethan Hein developed the pitch wheel in a similar attempt to arrive at minimalist representation of scales with an emphasis around effective pedagogy. While the pitch wheels are inherently an excellet way to represent, they still rely on interactive nature of a computer - something that I personally wish to minimize as much as possible.
- Pitch wheels have all the 12 notes. You can toggle each of these on and off to build a scale from bottom up
- Each note is color coded to provide a crude sense of emotion/tone color it is likely to evoke - sharps are brighter, and flats a bit dark
- By rotating a pitch wheel, you can preserve a scale but change it’s mode by simply shifting the root note
The Kekule Structure
My solution to this, interestingly, comes frome high-school chemistry.
‘I was sitting writing at my textbook; but the work did not progress; my thoughts were elsewhere. I turned my chair towards the fire and dozed. Again the atoms were gambolling before my eyes[…]But look! What was that? One of the snakes had seized hold of its own tail, and the form whirled mockingly before my eyes. As if by a flash of lightening I awoke; and this time I also spent the rest of the night in working out the consequences of the hypothesis.’ [August Kekulé, 1890]
-
There are speculations that Kekue’s ideas on representation of aromatic organic compounds is influenced, at least partly, by his youthful involvement in architecture.
-
While decades were spent understanding isomorphism of organic compounds, the conceptual leap from the idea of a carbon chain to the benzene ring is widely recognized as Kekule’s biggest achievement.
-
After iterating with sausage diagrams, he replaced it with a minimalist hexagon with double bonds. This also revealed interesting structures for di-substituted benzene, (ortho-, meta- and para- isomers)
-
Most organic chemists have adopted the hexagon as a convenient symbol
This method of representing modes is really a short hand method, and emphasizes on intervals more than individual notes in a 12 tone system.
How would this work?
- This type of notation fully acknoledges the circular nature of scales, superimposing octave with the root. The scales are hence represent to “wrap” around themselves, reflecting the fact that we hear note an octave apart as the same since they share majority of the overtones.
Step 1 - Draw a regular polygon with the same number of sides as the number of notes in your scale. A major scale is diatonic, so the polygon will be a regular heptagon. Be sure to align your polygon such that there is an apex. This apex will be the root note.
Step 2 - Next, starting from the top and moving clockwise, we denote every edge with a “double bond”, and half steps with a “single bond”. Our major scale would hence have 5 whole steps and 2 half
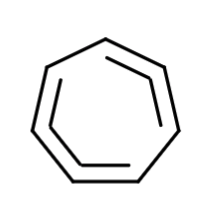
A minor scale has the same number of whole and half steps, but the sequence would look like
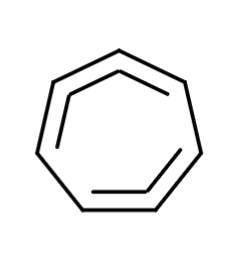
Step 3 - Label the apex with the root note of your scale. Let is pick C major for our example.
Symmetric Scales
A whole tone scale would look like:
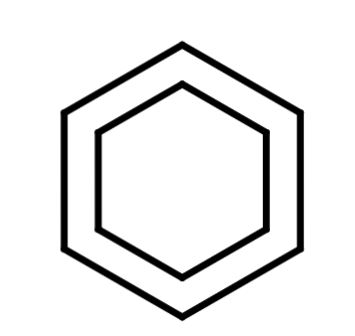
A double-diminshed octatonic scale comes in 2 modes of transposition. They can look like this
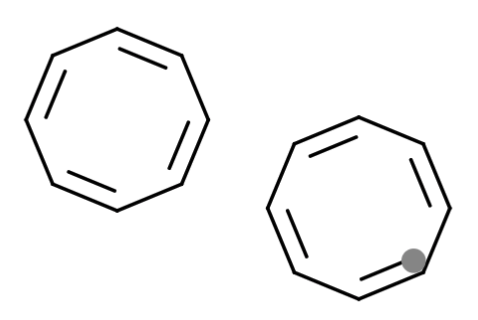
Further thoughts
-
Modes of a scale are technically isomers obtained by rotating a scale-ring.
-
Modulation can be visualized as a system of two rings with connected vertex or ege
-
This representation offers a bird’s eye view of composition as a system. This is especially useful when you need to improvise over a system of harmonies
-
Do symmetric scales in this representation have some kind of mesomeric effect?
-
How can modal substitutions be visualized?
-
Use chem doodle to draw diagrams?